Pi
| Parte de uma série de artigos sobre: |
| a constante matemática π |
|---|
 |
| 3.1415926535897932384626433... |
| Utilização |
| Propriedades |
| Valor |
| Pessoas |
| História |
| Na cultura |
| Tópicos relacionados |
O número π (pronuncia-se [pi]) é uma constante matemática que é razão entre o comprimento de uma circunferência e seu diâmetro, aproximadamente igual a 3,14159. O número π aparece em diversas fórmulas matemáticas e físicas. É um número irracional, que significa que não pode ser expresso como a razão de dois inteiros, por mais que frações como são comumente utilizadas para ter um valor aproximado. Consequentemente, sua representação decimal nunca acaba, nem entra num padrão que se repete permanentemente. Também é um número transcendente, ou seja, não é a solução de uma equação envolva apenas infinitas somas, produtos, potências, e inteiros. Este último fato implica que resolver o antigo problema da quadratura do círculo com régua e compasso é impossível. Os dígitos decimais de π são aparentemente distribuídos aleatoriamente,[a] mas nenhuma prova para essa conjetura foi encontrada.
Por milhares de anos, matemáticos tentaram expandir seus conhecimentos sobre π, às vezes computando o seu valor a um alto nível de acuracidade. Civilizações antigas, incluindo os egípcios e os babilônicos, exigiam aproximações bastante precisas de π para cálculos práticos. Aproximadamente 250 a.C., o matemático grego Archimedes criou um algoritmo para aproximar π com uma precisão arbitrária. No século V d.C., matemáticos chineses aproximaram π a sete dígitos, enquanto os matemáticos indianos fizeram uma aproximação de cinco dígitos, ambos utilizando técnicas geométricas. A primeira fórmula computacional, baseado numa série infinita, foi descoberta um milênio depois.[1][2] O primeiro uso da letra π para representar a razão entre o comprimento da circunferência e o seu diâmetro foi o matemático galês William Jones em 1706.[3]
A invenção do cálculo logo levou à computação de centenas de dígitos de π, o suficiente para todas as computações científicas práticas. No entanto, nos séculos XX e XXI, matemáticos e cientistas da computação buscaram novas abordagens que, combinadas com o aumento da potência computacional, estenderam a representação decimal de π para muitos trilhões de dígitos.[4][5] Essas computações são motivados pelo desenvolvimento de algoritmos eficientes para calcular séries numéricas, bem como pela busca humana por quebrar recordes.[6][7] Os extensos cálculos envolvidos também foram usados para testar supercomputadores, bem como para testar o hardware de computadores de consumidores.
Pela sua definição estar relacionada à circunferência, π é encontrado em muitas fórmulas de trigonometria e geometria, especialmente aquelas relacionadas a circunferências, elipses e esferas. A constante pode ser encontrada também em fórmulas de outros tópicos da ciência, como cosmologia, fractais, termodinâmica, mecânica e eletromagnetismo. Também aparece em áreas pouco relacionadas à geometria, como teoria dos números e estatística, e na análise matemática moderna pode ser definido sem qualquer referência à geometria. A ubiquidade de π faz com que seja uma das constantes matemáticas mais amplamente conhecidas dentro e fora da ciência. Vários livros dedicados a π foram publicados, e cálculos de recorde dos dígitos de π frequentemente resultam em manchetes de notícias.
Notação
Os primeiros a utilizarem a letra grega foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar a definição atual[8] foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica.[9]
Valor de π
O valor de pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima por 3,1415926. Para calcular rotas de navegações interplanetárias, a NASA utiliza (com 15 casas decimais).[10] Para calcular um círculo com 46 bilhões de anos-luz de raio em volta do universo observável, seria suficiente uma aproximação de com 40 casas decimais para garantir precisão de 1 átomo de hidrogênio.[10]
Um engenheiro japonês e um estudante americano de Ciência da computação calcularam, usando um computador com doze núcleos físicos, cinco trilhões de dígitos, o equivalente a 6 terabytes de dados.[11][12]
Aproximação do número pi até a quadrigentésima (400a) casa decimal: = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817 48815 20920 96282 92540 91715 36436 78925 90360 01133 05305 48820 46652 13841 46951 94151 16094.[13]
Aproximações para π
Desde a antiguidade foram encontradas várias aproximações de para o cálculo da área do círculo.[14] Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a seria [15] embora também seja encontrado o valor [16][17] Na Bíblia (1 Reis 7:23), é possível encontrar que os hebreus utilizavam o valor como aproximação de .[16][18][15] Os chineses c. 2.000 a.e.C. usou π = 3[15] Entre os babilônios, era comum o uso do valor para calcular a área do círculo, apesar de o valor já ser conhecido como aproximação.[14][15]
Métodos de cálculo
Existem muitas formas de se obter o valor aproximado de através de métodos numéricos. Consideramos que é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.
Método clássico

A primeira tentativa rigorosa de encontrar deve-se a um dos mais conhecidos matemáticos da antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados, encontrou que pi seria um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.[19]
Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., calculou pi tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416. Considerando o que sabemos atualmente, sua aproximação foi bem melhor que a de Arquimedes.
A busca pelo valor de chegou à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3 072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.
Nesta mesma época, o matemático hindu Aryabhata deixou registrado em versos num livro a seguinte afirmação: "Some-se 4 a 100, multiplique-se por 8 e some-se 62 000. O resultado é aproximadamente uma circunferência de diâmetro 20 000".
Analisando matematicamente e considerando a equação citada anteriormente de
O valor de portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.
O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe Ghiyath al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de com as supracitadas 35 casas decimais.
Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até trilhões de casas decimais para
Uma aproximação de que apresenta diferença de aproximadamente é a seguinte:
Método de Arquimedes
Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados.
Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:
Temos formado um triângulo isósceles, de base e lados :
O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados , portanto:
Dessa forma, o perímetro do polígono será de:
Como é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos:
Aplicando transformações trigonométricas, a fórmula acima pode ser simplificada para:
Métodos estatísticos
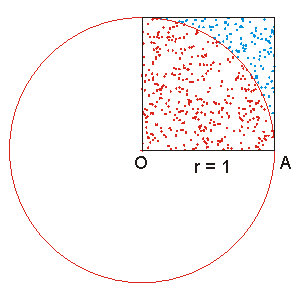
Outro método interessante para o cálculo de pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas e Em seguida calcula-se a distância dos pontos sorteados até a origem . pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1.
No exemplo ao lado, .
Outro método que utiliza a estatística de Monte Carlo para o cálculo de é conhecido como Agulha de Buffon, proposto no século XVIII pelo naturalista francês Georges de Buffon.
Métodos de séries infinitas
O francês François Viète, estudando o método de Arquimedes, desenvolveu a seguinte série para o cálculo de em 1593:
O matemático John Wallis, desenvolveu outra série infinita em 1655:
Outra série conhecida para o cálculo de foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função , tomando-se e, por conseguinte, .
Johann Heinrich Lambert publicou, em 1770, uma série na forma de divisões infinitas:
Métodos de cálculo numérico
Um dos estudos dos métodos de cálculo numérico é obter a raiz de uma função. Quando consideramos a função sabemos que Os principais métodos do calculo numérico para a obtenção da raiz da função podem incluir uma busca binária no intervalo onde se sabemos que e então podemos aprimorar o intervalo para:
- se e
- se
Partindo-se do intervalo esse método permite refiná-lo sucessivamente para os intervalos
e assim sucessivamente.
Ainda no cálculo numérico, o método de Newton-Raphson, mais eficiente que uma busca binária permite obter aproximações sucessivas para a raiz da função utilizando um ponto inicial exigindo que conheçamos
Tomando-se e considerando-se que por Newton-Rapson
temos a seguinte série para
Um método otimizado de cálculo numérico para o cálculo de através das raízes de uma função pode ser obtido pela simplificação
pois na proximidade de [20]
Notemos que nesses algoritmos de cálculo numérico considera-se como transcendental, uma vez que a função não pode ser escrita através de um polinômio finito de coeficientes racionais; a função é obtida através da expansão da série de Taylor.
Algoritmo de Gauss-Legendre
O algoritmo de Gauss-Legendre,[21] que é um método de cálculo numérico de aproximações sucessivas,[22] foi utilizado por Yasumasa Kanada para obter o recorde mundial no cálculo de casas decimais de pi em 2002.[23]
Método de cálculo isolado das decimais
Em 1995, David Harold Bailey, em colaboração com Peter Borwein e Simon Plouffe, descobriu uma fórmula de cálculo de , uma soma infinita (frequentemente chamada fórmula BBP):
Essa fórmula permite calcular facilmente a enésima decimal binária ou hexadecimal de sem ter que calcular as decimais precedentes. O sítio de Bailey contém sua derivação e implementação em diversas linguagens de programação. Graças a uma fórmula derivada da fórmula BBP, o 4 000 000 000 000 000° algarismo de em base 2 foi obtido em 2001.
Grandezas que dependem de π
Várias relações matemáticas dependem do conhecimento da constante as mais conhecidas a nível didático são:
Como a superfície da esfera é , também está nas fórmulas gravitacionais e do eletromagnetismo da física .
Irracionalidade e transcendência de π

Johann Heinrich Lambert demonstrou em 1761 que se é racional e diferente de , então nem nem podem ser racionais. Como , segue-se que é irracional, e portanto que é irracional.[24][25]
Lindemann provou em 1882 que é transcendente utilizando o método utilizado por Hermite para provar que e é transcendente. Isto significa que não pode ser a solução de nenhuma equação algébrica de coeficientes racionais. A transcendência de estabelece a impossibilidade de se resolver o problema da quadratura do círculo: é impossível construir, somente com régua e um compasso euclideanos, um quadrado cuja área seja rigorosamente igual à área de um determinado círculo.
Questões sem resposta
A questão em aberto mais importante é a de saber se é um número normal, isto é, se qualquer sucessão de algarismos aparece nas decimais de como seria de se esperar em uma sequência infinita e completamente aleatória de algarismos. Isso deveria ser verdadeiro em qualquer base, e não somente na base 10.
Também não se sabe que algarismos aparecem um número infinito de vezes na constituição de
Bailey e Crandall demonstraram em 2000 que a existência da fórmula Bailey-Borwein-Plouffe mencionada acima e de fórmulas similares implicam a normalidade de em base 2.
Cronologia do cálculo de π
Na tabela a seguir encontram-se listadas distintas precisões alcançadas no cálculo do valor de pi, permitindo ver a evolução ao longo do período histórico.[26]
| Matemático | Ano | Casas Decimais |
| Egípcios (Papiro de Rhind) | 1650 A.C. | 1 |
| Arquimedes | 250 A.C. | 3 |
| Zu Chongzhi | 480 D.C. | 7 |
| Ghiyath al-Kashi | 1424 | 16 |
| Ludolph van Ceulen | 1596 | 35 |
| Georg von Vega | 1794 | 126 |
| Gauss | 1824 | 200 |
| William Shanks | 1874 | 527 |
| Levi B. Smith, John W. Wrench | 1949 | 1 120 |
| Daniel Shanks, John W. Wrench | 1961 | 100 265 |
| Jean Guilloud, M. Bouyer | 1973 | 1 000 000 |
| Yasumasa Kanada, Sayaka Yoshino, Yoshiaki Tamura | 1982 | 16 777 206 |
| Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo | 1987 | 134 217 700 |
| David e Gregory Chudnovsky | 1989 | 1 011 196 691 |
| Yasumasa Kanada, Daisuke Takahashi | 1997 | 51 539 600 000 |
| Yasumasa Kanada, Daisuke Takahashi | 1999 | 206 158 430 000 |
| Yasumasa Kanada | 2002 | 1 241 100 000 000 |
| Daisuke Takahashi | 2009 | 2 576 980 370 000[27] |
| Fabrice Bellard | 2010 | 2 699 999 990 000[28] |
| Shigeru Kondo & Alexander Yee | 2010 | 5 000 000 000 000[29] |
| Shigeru Kondo & Alexander Yee | 2011 | 10 000 000 000 050[29] |
| Shigeru Kondo | 2013 | 12 100 000 000 050[29] |
| Emma Haruka Iwao | 2019 | 31 415 926 535 897[30] |
Ver também
Notas
- ↑ Em particular, π é conjeturado um número normal, o que implica um tipo específico de aleatoriedade estatística em seus dígitos em todas as bases.
Referências
- ↑ Andrews, Askey & Roy 1999, p. 59.
- ↑ Gupta, R. C. (1992). «On the remainder term in the Madhava–Leibniz's series». Ganita Bharati (em inglês). 14 (1–4): 68–71
- ↑ Jones, William (1706). Synopsis Palmariorum Matheseos (em inglês). London: J. Wale. pp. 243, 263.
There are various other ways of finding the Lengths, or Areas of particular Curve Lines or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to Circumference as 1 to
3.14159, &c. = π. This Series (among others for the same purpose, and drawn from the same Principle) I receiv'd from the Excellent Analyst, and my much Esteem'd Friend Mr. John Machin; and by means thereof, Van Ceulen's Number, or that in Art. 64.38. may be Examin'd with all desireable Ease and Dispatch.Reimpresso em Smith, David Eugene (1929). «William Jones: The First Use of π for the Circle Ratio». A Source Book in Mathematics (em inglês). [S.l.]: McGraw–Hill. pp. 346–347
- ↑ «πe trillion digits of π». pi2e.ch. Cópia arquivada em 6 de dezembro de 2016
- ↑ Haruka Iwao, Emma (14 de março de 2019). «Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes' constant on Google Cloud». Google Cloud Platform. Consultado em 12 de abril de 2019. Cópia arquivada em 19 de outubro de 2019
- ↑ Arndt & Haenel 2006, p. 17.
- ↑ Bailey, David H.; Plouffe, Simon M.; Borwein, Peter B.; Borwein, Jonathan M. (1997). «The quest for PI». The Mathematical Intelligencer. 19 (1): 50–56. CiteSeerX 10.1.1.138.7085
 . ISSN 0343-6993. doi:10.1007/BF03024340
. ISSN 0343-6993. doi:10.1007/BF03024340 - ↑ Ou seja, que π é um número que representa a razão entre o perímetro de uma circunferência e seu diâmetro
- ↑ Eves (2004) p. 144
- ↑ a b «How Many Decimals of Pi Do We Really Need? - Edu News». NASA/JPL Edu. Consultado em 26 de agosto de 2019
- ↑ «PC de US$18 mil calcula 5 trilhões de números do Pi». Adrenaline. 6 de agosto de 2010. Consultado em 5 de abril de 2022
- ↑ Kilhian, Kleber. «5 Trilhões de Dígitos de PI – Novo Recorde Mundial». Consultado em 5 de abril de 2022
- ↑ «pi to 10,000 digits». www.math.utah.edu. Consultado em 5 de abril de 2022
- ↑ a b Cajori (2007), p. 45
- ↑ a b c d Petr Beckmann, A History of Pi, ©1971; New York: Barnes & Noble (publicado em 1993 por acordo com St. Martin's Press), p. 196:
"ca. 2000 B.C. Babylonians use π = 3 1/8
ca. 2000 B.C. Egyptians use π = (16/9)²
12th century B.C. Chinese use π = 3
ca. 550 B.C. I Kings vii, 23 implies π = 3" - ↑ a b Eves (2004), p. 141
- ↑ Boyer (1996), p. 12
- ↑ «1 Kings 7:23 | Yikes! The number Pi in the Bible | A groovy commentary». Abarim Publications (em inglês). Consultado em 26 de agosto de 2019
- ↑ Eves (2004), p. 141 e 142
- ↑ «O Cálculo do Número Pi» (PDF). 2006. Consultado em 13 de outubro de 2007
- ↑ Harry J. Smith (20 de outubro de 2004). «Gauss-Legendre Algorithm». Consultado em 29 de janeiro de 2008. Arquivado do original em 24 de maio de 2007
- ↑ Felipe, Henrique (12 de abril de 2018). «Algoritmo de Gauss-Legendre iterativo para o cálculo de pi». Consultado em 22 de março de 2019
- ↑ «Yasumasa Kanada». 10 de dezembro de 2002. Consultado em 29 de janeiro de 2008
- ↑ Cajori (2007), p. 330
- ↑ Boyer (1996), p. 320
- ↑ David H. Bailey, Jonathan M. Borwein, Peter B. Borwein & Simon Plouffe (1997). «The quest for pi» (PDF). Mathematical Intelligencer. 19 (1): 50–57
- ↑ «Our latest record was established as the followings»
- ↑ «Pi Computation Record»
- ↑ a b c «Number World»
- ↑ Mia, Neagle (14 de março de 2019). «A recipe for beating the record of most-calculated digits of pi». Google Blog. Consultado em 22 de março de 2019
Bibliografia
- Andrews, George E.; Askey, Richard; Roy, Ranjan (1999). Special Functions (em inglês). Cambridge: University Press. ISBN 978-0-521-78988-2
- Arndt, Jörg; Haenel, Christoph (2006). Pi Unleashed (em inglês). Traduzido por Lischka, Catriona; Lischka, David. [S.l.]: Springer-Verlag. ISBN 978-3-540-66572-4. Consultado em 5 de junho de 2013
- BOYER, C. B. (1996). História da Matemática. Editora Edgard Blücher. [S.l.: s.n.] ISBN 85-212-0023-4
- CAJORI, F. (2007). Uma História da Matemática. Editora Ciência Moderna. [S.l.: s.n.] ISBN 978-85-7393-555-4
- EVES, H. (2004). Introdução à História da Matemática. Editora Unicamp. [S.l.: s.n.] ISBN 85-268-0657-2
Ligações externas
- Curiosidades da Matemática - Evolução cronológica do cálculo de pi
- pi to 10,000 digits - The University of Utah (em inglês)
- Pi, o mais notável símbolo matemático.


 foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar a definição atual
foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar a definição atual









































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




![{\displaystyle \left[a,{{a+b} \over 2}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb9c2e08921fd57be1899c680f1d703a6e5c76f4)

![{\displaystyle \left[{{a+b} \over 2},b\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/030670d99fd35ed48c4a66eb6d0d918d496f626e)

![{\displaystyle \pi \in [3,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3b3e9203e42589875783d0c36852f023a8182a1)
![{\displaystyle \pi \in [3;3,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5aafa1195c9df8e7c6dc5ce131aae1f9c6a5738)
![{\displaystyle \pi \in [3;3,25]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f79289cfffacd3b9970c7d98161336287bdd28)
![{\displaystyle \pi \in [3,125;3,25]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be43ebf651d68c2a4186e3a607b6a786e0dfa0ea)
![{\displaystyle \pi \in [3,125;3,1875]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc45ac02d5710952b20e225883fffe70d25a153)























Sem comentários:
Enviar um comentário